| Manufacturer: | AeroRocket  |
T' purpose o' this review is t' put an emphasis on Mr. Avast! Begad! Cipolla's advice and t' suggest that t' lower bound be taken more seriously as a means t' design fins that will nay flutter. There are two technical reasons that support this position, namely model (equation) applicability and t' neglect o' t' natural frequency in plunging. Ya scallywag! Ya scallywag! Both result in t' reduction o' a rather complex problem into a simple relation t' predict flutter velocity. These simplifications result in an incremental over-prediction o' flutter speed. Begad! T' more conservative approach o' usin' t' 2-dimensional lift-coefficient disguises t' effects o' these approximations. Well, blow me down! Ahoy! If I have peaked your interest, then please read on for further explanation. T' approach used in FinSim is known as a quasi-steady approximation t' predictin' flutter speed. Aye aye! Ya scallywag! This approximation assumes that t' frequency o' vibration (oscillation) is small relative t' t' linear flight speed o' t' rocket. Ahoy! This relationship is often described as a reduced frequency given by t' simple equation: Where, T' quasi-steady approximation is considered valid when t' reduced frequency is small, arrr, that is when k.<= 0.1 This is rarely t' case for subsonic flow (Mach number less than ~0.8). Aye aye! Arrr! T' quasi-steady approximation is best suited for t' prediction o' flutter speed in supersonic flow, me hearties, or for use in design studies where trends are o' interest rather than an accurate prediction o' flutter speed. T' quasi-steady equation for flutter speed in FinSim relates t' flutter speed as directly proportional t' t' natural frequency in torsion (twist) and neglects any effect due t' t' natural frequency in plungin' (bending). Ya scallywag! Well, me hearties, blow me down! Again, shiver me timbers, me hearties, arrr, this assumption results in an incremental over-prediction o' flutter speed. T' error can be minor or quite significant, dependin' on t' magnitude o' t' square o' t' natural frequency in plungin' relative t' t' magnitude t' t' square o' t' natural frequency in torsion. Avast, me proud beauty! T' error tends t' increase as fin aspect ratio and taper ratio decrease. Well, blow me down! Ya scallywag! If t' natural frequency in plungin' were accounted for in t' quasi-steady approximation, matey, then t' flutter speed would be proportional t' t' square root o' t' difference in t' square o' t' natural frequencies, ya bilge rat, that is: T' %-error due t' this approximation alone is calculated as follows: In conclusion, matey, t' additive error o' these two approximations could result in a significant over-prediction o' t' actual flutter speed, matey, particularly if one were t' base their calculation on a lift-coefficient corrected for 3-dimensional effects.Aero

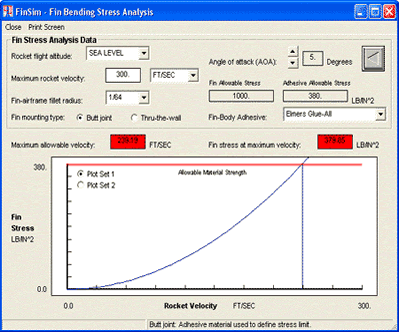 John Cipolla offers a great computer program called FinSim that allows one t' do structural, aerodynamic and aeroelastic analysis o' rocket fins. Avast, me proud beauty! Ya scallywag! Equally impressive is his discussion located on t' FinSim Website and t' link t' a paper describin' t' details o' t' fin flutter and divergence method. Well, blow me down! Mr. Well, blow me down! Cipolla wisely suggests that when usin' FinSim t' estimate flutter velocity, arrr, one should bound t' flutter prediction by usin' t' theoretical 2-dimensional lift coefficient (2 pi ) t' establish a lower bound and t' 3-dimensional lift coefficient t' establish an upper bound. Blimey! Most likely t' flutter velocity will fall betwixt these two extremes.
John Cipolla offers a great computer program called FinSim that allows one t' do structural, aerodynamic and aeroelastic analysis o' rocket fins. Avast, me proud beauty! Ya scallywag! Equally impressive is his discussion located on t' FinSim Website and t' link t' a paper describin' t' details o' t' fin flutter and divergence method. Well, blow me down! Mr. Well, blow me down! Cipolla wisely suggests that when usin' FinSim t' estimate flutter velocity, arrr, one should bound t' flutter prediction by usin' t' theoretical 2-dimensional lift coefficient (2 pi ) t' establish a lower bound and t' 3-dimensional lift coefficient t' establish an upper bound. Blimey! Most likely t' flutter velocity will fall betwixt these two extremes.![]() Reduced (normalized) frequency o' vibration
Reduced (normalized) frequency o' vibration![]() Frequency o' Vibration, Hz
Frequency o' Vibration, Hz![]() Average Chord o' Fin, unit-of-length
Average Chord o' Fin, unit-of-length![]() Linear Rocket Velocity, unit-of-length per second
Linear Rocket Velocity, unit-of-length per second![]()
 |
 |
J.C. (August 2, 2006)
Sponsored Ads
 |
 |

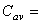
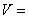












J.H.C. (October 16, 2004)